Research - Optical and Quantum Communications Group
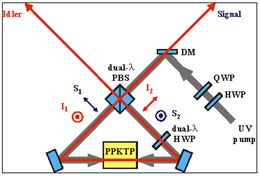
Sources of Polarization-Entangled Photons
Polarization-entangled photons are essential resources for many quantum information science applications, such as quantum key distribution and linear optics quantum computing. Compact, high-flux sources of high-quality polarization-entangled photons are desirable for implementing these applications. In designing our entanglement sources we take advantage of advances in nonlinear crystals and utilize some of the standard techniques in nonlinear optics. The method of quasi-phase matching in periodically-poled potassium titanyl phosphate (PPKTP) and periodically-poled lithium niobate (PPLN) enables efficient downconversion at user-specified wavelengths, and collinearly propagating geometry in PPKTP and PPLN allows efficient collection of output photons. We have implemented a continuous-wave (cw) PPKTP polarization Sagnac interferometer as a spectrally bright source of polarization-entangled photons yielding 10,000 detected pairs/s/mW of pump power in a 1-nm bandwidth with a quantum-interference visibility of 98%. A pulsed version of the PPKTP Sagnac source is under development for use in free-space quantum key distribution. We are also working on a wavelength-nondegenerate PPLN Sagnac source that is expected to show a ten-fold increase in pair generation efficiency that can be used to characterize high-speed single-photon counters.

Fuchs-Peres-Brandt Attack on Quantum Key Distribution
Fuchs and Peres described the most general way in which an individual attack could be mounted against single-photon, polarization-based Bennett-Brassard 1984 quantum key distribution. Eve interacts a probe photon with Alice’s photon in a unitary manner, then sends Alice’s photon to Bob, and performs a probability operator-valued measurement on her probe photon. Slutsky et al. demonstrated that the Fuchs-Peres construct — with the appropriate choice of probe state, interaction, and measurement — affords Eve the maximum amount of Rényi information about the error-free sifted bits that Bob receives for a given level of disturbance. Brandt extended the Slutsky et al. treatment by showing that the optimal probe could be realized with a single controlled-NOT (CNOT) gate. We then showed how a complete physical simulation of the Fuchs-Peres-Brandt (FPB) probe could be accomplished using single-photon two-qubit (SPTQ) quantum logic. We have implemented that experiment and are collecting data that will permit a full exploration of the power of the FPB probe.
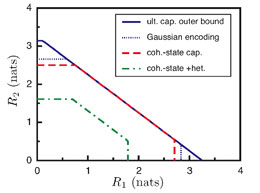
Classical Information-Carrying Capacity of Bosonic Channels
The lossy bosonic channel provides a quantum model for optical communication systems that rely on fiber or free-space propagation. For the pure-loss case, we have shown that the classical information-carrying capacity of this channel is achievable with single-use coherent-state encoding. For the more general thermal-noise channel, the Holevo information of single-use coherent-state encoding is a lower bound on the channel capacity, which we have shown would equal that capacity if our recent conjecture about that channel’s minimum output entropy were correct. We have studied multiple-access bosonic communications, in which two or more senders communicate to a common receiver over a shared propagation medium. We showed that single-use coherent-state encoding with the optimum measurement achieves the sum-rate capacity but does not realize the single-user capacity, and we quantified the capacity region that is lost when coherent (heterodyne or homodyne) detection is employed instead of the optimum measurement. We are now considering the classical information-carrying capacity of the degraded bosonic broadcast channel, in which a single sender communicates to two or more receivers through a lossless 1:M coupler whose auxiliary inputs are in their vacuum states.
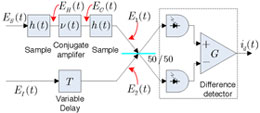
Optical Coherence Tomography with Classical Phase-Sensitive Light
Optical coherence tomography (OCT) produces 3-D imagery through focused-beam scanning (for transverse resolution) and interference measurements (for axial resolution). Quantum optical coherence tomography (Q-OCT) offers a factor-of-two improvement in axial resolution and the advantage of even-order dispersion cancellation when it is compared to conventional OCT (C-OCT). These features have been ascribed to the non-classical nature of the biphoton state employed in former, as opposed to the classical state used in the latter. We have introduced a new OCT configuration, called phase-conjugate OCT (PC-OCT), which shows that non-classical light is not necessary to reap Q-OCT’s advantages. PC-OCT uses classical-state signal and reference beams, which have a phase-sensitive cross-correlation, together with phase conjugation to achieve the axial resolution and even-order dispersion cancellation of Q-OCT with a signal-to-noise ratio that can be comparable to that of C-OCT.

Quantum Theory of Cross-Phase Modulation
Chuang and Yamamoto showed that the cross-Kerr effect (cross-phase modulation) could be used, in principle, to create an optical CNOT gate in dual-rail quantum logic, thus completing a universal gate set for all-optical quantum computation. They used a single-mode model for the cross-phase modulation interaction, and presumed that a single photon propagating in one mode of a dual-rail qubit could induce a p-rad phase shift on a single photon propagating in one mode of another dual-rail qubit. We have used multi-mode continuous-time analysis to show that the causal, non-instantaneous behavior of any c(3) nonlinearity is enough to preclude high-fidelity operation of such a gate, owing to the phase noise that is required by commutator-bracket preservation. We are now exploring the limitations this noise imposes on quantum computation architectures that rely on weak nonlinearities, and we are studying the relationship between our theory and cross-phase modulation created via electromagnetically-induced transparency.
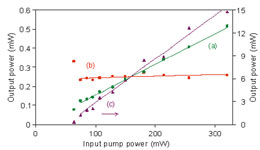
Optical Frequency Division
Since the introduction of octave-spanning femtosecond comb technology, optical frequency measurements can now be routinely performed using the regularly-spaced comb lines as frequency markers. The comb-based measurement capability can be further enhanced by a 3-to-1 optical frequency divider that provides three strong frequency markers at f, 2f, and 3f, where 3f is the pump frequency for a 3-to-1 optical parametric oscillator (OPO) with outputs at f and 2f. The f and 2f frequency markers can be used to lock two optical frequency combs centered at different spectral regions, thus creating a phase-locked multi-octave-spanning comb. We have utilized a double-grating PPLN crystal to implement the 3-to-1 OPO, and preliminary results show self-phase locking at the f-2f-3f operating point. In the same apparatus we have discovered a novel cascaded parametric oscillation process in which the signal field of the primary parametric oscillator pumps the secondary parametric oscillator. Above the secondary threshold, the primary signal power is clamped and all the other output powers increase linearly with the input pump power, unlike the square-root dependence in a conventional OPO, thus providing a convenient and efficient way to generate multiple tunable outputs.
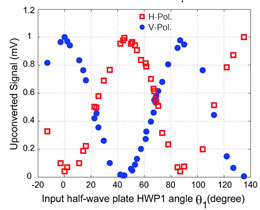
Quantum-State Frequency Conversion
Our architecture for long-distance quantum communication relies on fiber-optic transmission of polarization-entangled photons from a dual parametric amplifier source to a pair of trapped Rb atom quantum memories. The protocol requires a high-flux continuous-wave source of polarization-entangled photons at 795 nm and 1.55 mm, for the loading of local and remote quantum memories, respectively. Out of each pair of entangled photons produced by the source, one of the photons is sent to Alice’s local station while the conjugate photon travels over standard telecommunication fiber to Bob’s remote receiver node. In order to load the remotely-located memory, quantum-state frequency conversion is required, so that the polarization state of the 1.55 mm photon is transferred to a 795 nm photon. This form of frequency upconversion must function down to the single photon level with low insertion loss, while providing both high conversion efficiency and high-fidelity preservation of arbitrary polarization states. We have demonstrated 90%-efficient single-photon frequency upconversion for a single polarization, using a bulk periodically-poled lithium niobate (PPLN) crystal embedded in a pump enhancement ring cavity. We have also demonstrated 50%-efficient polarization-preserving upconversion in a novel bidirectional PPLN upconverter whose performance was pump power limited.

