Yoav Lahini1, Gregory R. Steinbrecher, Adam D. Bookatz and Dirk Englund
doi:10.1038/s41534-017‑0050‑2
Abstract:
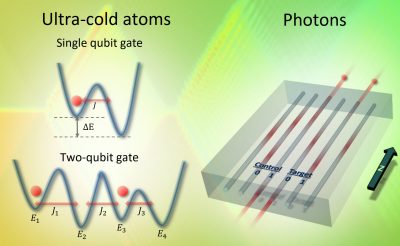
Quantum Walks are unitary processes describing the evolution of an initially localized wavefunction on a lattice potential. The complexity of the dynamics increases significantly when several indistinguishable quantum walkers propagate on the same lattice simultaneously, as these develop non-trivial spatial correlations that depend on the particle’s quantum statistics, mutual interactions, initial positions, and the lattice potential. We show that even in the simplest case of a quantum walk on a one dimensional graph, these correlations can be shaped to yield a complete set of compact quantum logic operations. We provide detailed recipes for implementing quantum logic on one-dimensional quantum walks in two general cases. For non-interacting bosons—such as photons in waveguide lattices—we find high-fidelity probabilistic quantum gates that could be integrated into linear optics quantum computation schemes. For interacting quantum-walkers on a one-dimensional lattice—a situation that has recently been demonstrated using ultra-cold atoms—we find deterministic logic operations that are universal for quantum information processing. The suggested implementation requires minimal resources and a level of control that is within reach using recently demonstrated techniques. Further work is required to address error-correction.
