MASSACHUSETTS INSTITUTE OF TECHNOLOGY, INSTITUTE FOR SOLDIER NANOTECHNOLOGIES
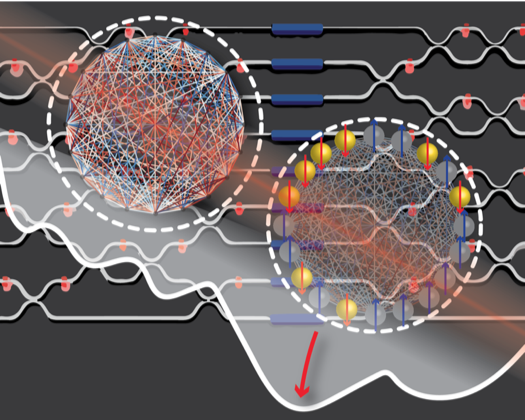 Artistic illustration of solving complex problems with a photonic circuit. The background pattern shows a network of interferometers able to perform arbitrary unitary matrix multiplication. By encoding the problem data into the weights of the optical matrix and letting an optical signal evolve through the optical circuit, one can find the state minimizing the energy of the associated problem (the solution). In the case of the Ising problem, the solution is a given distribution of spins that can only take binary values. Image courtesy of the researchers.
Artistic illustration of solving complex problems with a photonic circuit. The background pattern shows a network of interferometers able to perform arbitrary unitary matrix multiplication. By encoding the problem data into the weights of the optical matrix and letting an optical signal evolve through the optical circuit, one can find the state minimizing the energy of the associated problem (the solution). In the case of the Ising problem, the solution is a given distribution of spins that can only take binary values. Image courtesy of the researchers.
Many of the most challenging optimization problems encountered in various disciplines of science and engineering, from biology and drug discovery [1] to routing and scheduling [2] can be reduced to NP-complete problems. Intuitively speaking, NP-complete problems are “hard to solve” because the number of operations that must be performed in order to find the solution grows exponentially with the problem size. The ubiquity of NP-complete problems has led to the development of dedicated hardware (such as optical annealing and quantum annealing machines like “D‑Wave”) and special algorithms (heuristic algorithms like simulated annealing).
Recently, there has been a growing interest in solving these hard combinatorial problems by designing optical machines. These optical machines consist of a set of optical transformations imparted to an optical signal, so that the optical signal will encode the solution to the problem after some amount of computation. Such machines could benefit from the fundamental advantages of optical hardware integrated into silicon photonics, such as low-loss, parallel processing, optical passivity at low optical powers and robust scalability enabled by the development of fabrication processes by the industry. However, the development of compact and fast photonic hardware with dedicated algorithms which optimally utilize the capability of this hardware, has been lacking.
Today, the path to solving NP-complete problems with integrated photonics is open due to the work of Charles Roques-Carmes, Dr. Yichen Shen, Cristian Zanoci, Mihika Prabhu, Fadi Atieh, Dr. Li Jing, Dr. Tena Dubček, Chenkai Mao, Miles Johnson, Prof. Vladimir Čeperić, Prof. Dirk Englund, Prof. John Joannopoulos, and Prof. Marin Soljačić from MIT and the Institute for Soldier Nanotechnologies, published in Nature Communications [3]. In this work, the MIT team developed an algorithm dedicated to solving the well-known NP-complete Ising problem with photonics hardware.
Originally proposed to model magnetic systems, the Ising model describes a network of spins that can point only up or down. Each spin’s energy depends on its interaction with neighboring spins — in a ferromagnet, for instance, the positive interaction between nearest neighbors will incentivize each spin to align with its closest neighbors. An Ising machine will tend to find the spin configuration that minimizes the total energy of the spin network. This solution can then be translated into the solution of other optimization problem [4].
Heuristic Ising machines, like the one developed by the MIT team, only yields a candidate solution to the problem (which is, on average, close to the optimal solution). However, algorithms that always find the exact solution to the problem are difficult to apply to large problem sizes, as they would often have to run for hours, if not days, to terminate. Therefore, heuristic algorithms are an alternative to exact algorithms, since they provide fast and cheap solutions to hard problems.
The researchers were guided by their knowledge of fundamental photonics. Professor Marin Soljačić from MIT explains: “Optical computing is a very old field of research. Therefore, we had to identify which recent advances in photonic hardware could make a difference. In other words, we had to identify the value proposition of modern photonics.” Graduate student Charles Roques-Carmes adds: “We identified this value proposition to be: (a) performing fast and cheap fixed matrix multiplication and; (b) performing noisy computation, which means that the result of the computation slightly varies from one run to the other, a little bit like flipping a coin. Therefore, these two elements are the building blocks of our work.”
While developing this algorithm and benchmarking it on various problems, the researchers discovered a variety of related algorithms that could also be implemented in photonics to find solutions even faster. Postdoctoral associate Dr. Yichen Shen is enthusiastic about the prospect of this work: “The field of enhancing computing capability with integrated photonics is currently booming, and we believe this work can be part of it. Since the algorithm we developed optimally leverages the strengths and weaknesses of photonic hardware, we hope it could find some short-term application.” The MIT research team is currently working in collaboration with others towards realizing proof-of-concept experiments and benchmarking their algorithm on photonic hardware, versus other photonic machines and conventional algorithms running on computers.
This work was supported in part by the Semiconductor Research Corporation (SRC) under SRC contract #2016-EP-2693‑B (Energy Efficient Computing with Chip-Based Photonics MIT). This work was supported in part by the National Science Foundation (NSF) with NSF Award #CCF-1640012 (E2DCA: Type I: Collaborative Research: Energy Efficient Computing with Chip-Based Photonics). This material is based upon work supported in part by the U.S. Army Research Laboratory and the U.S. Army Research Office through the Institute for Soldier Nanotechnologies, under contract number W911NF-18–2‑0048. C. Z. was financially supported by the Whiteman Fellowship. M. P. was financially supported by NSF Graduate Research Fellowship grant number 1122374.
Contact information:
Charles Roques-Carmes (chrc@mit.edu), Yichen Shen (ycshen@mit.edu), and Marin Soljačić (soljacic@mit.edu).
[1] For instance, the task of determining the three-dimensional structure of a protein, given its sequence of amino-acids.
[2] For instance, the problem of finding the shortest path connecting many cities.
[3] Charles Roques-Carmes, et al. Heuristic recurrent algorithms for photonic Ising machines. Nat Commun 11, 249 (2020) doi:10.1038/s41467-019–14096‑z
[4] One such procedure has been proposed by Karp in his seminal paper: Karp, Richard M. “Reducibility among combinatorial problems.” Complexity of computer computations. Springer, Boston, MA, 1972. 85–103.
